Kaggle competition Digit Recogniser-Part 1
This notebook is the first part of the Digit Recogniser kaggle competition. In this notebook pre-process the MNIST digit images to be used for building different models to recognize handwritten digits and we will build and train a Multiclass Logistic Regression model using the MNIST data.
** Note: ** The Microsoft Cognitive Toolkit (CNTK) is an open-source toolkit for commercial-grade distributed deep learning. We will be using cntk to build our model.
Introduction
Problem: Optical Character Recognition (OCR) is a hot research area and there is a great demand for automation. The MNIST data is comprised of hand-written digits with little background noise making it a nice dataset to create, experiment and learn deep learning models with reasonably small comptuing resources.
Goal: Our goal is to train a classifier that will identify the digits in the MNIST dataset.
Approach: There are 4 stages in this workflow:
- Data reading: We will use the CNTK Text reader.
- Data preprocessing: Store the data into cntk text file.
- Model creation: Multiclass Logistic Regression model.
- Train-Predict: Train the model using training dataset and predict output for test dataset.
# Import the relevant modules to be used later
from __future__ import print_function
import gzip
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import numpy as np
import os
import shutil
import struct
import sys
import cntk as C
try:
from urllib.request import urlretrieve
except ImportError:
from urllib import urlretrieve
# Config matplotlib for
Data Reading and visulization
We will load the data available from in our local machine. The MNIST database is a standard set of handwritten digits that has been widely used for training and testing of machine learning algorithms. It has a training set of 60,000 images and a test set of 10,000 images with each image being 28 x 28 grayscale pixels. This set is easy to use visualize and train on any computer.In our competition the training set contains 42000 greyscale images and test set comprises of 28000 images.
filename = 'train.csv'
raw_data = open(filename, 'rt')
train = np.loadtxt(raw_data,skiprows=1,dtype='int',delimiter=",")
print(train.shape)
(42000, 785)
filename = 'test.csv'
raw_data = open(filename, 'rt')
test = np.loadtxt(raw_data,skiprows=1,dtype='int',delimiter=",")
print(test.shape)
(28000, 784)
Here, we use matplotlib to display one of the training images and it’s associated label.
# Plot a random image
sample_number = 2018
plt.imshow(train[sample_number,1:].reshape(28,28), cmap="gray_r")
plt.axis('off')
print("Image Label: ", train[sample_number,0])
Image Label: 3
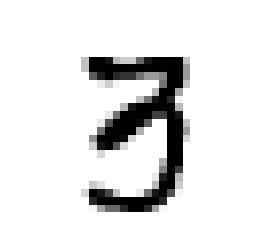
Data preprocessing
Understanding the dataset:
The training file is a csv format containing 785 columns which includes the labels.The rest 784 length vector can be seen as flattening the images to a vector (28x28 image pixels becomes an array of length 784 data points).

The labels are encoded as 1-hot encoding (label of 3 with 10 digits becomes 0001000000, where the first index corresponds to digit 0 and the last one corresponds to digit 9.

print(train[2018,1:])
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 62 254 253 234 71
51 51 152 233 254 253 254 253 62 0 0 0 0 0 0 0 0 0
0 0 0 0 0 61 253 252 253 252 253 252 253 252 253 252 253 252
102 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 163 223
254 213 203 203 142 102 102 122 254 253 102 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 20 50 10 0 0 0 0 0 142
253 252 61 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 72 253 254 91 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 62 142
233 252 213 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 72 233 254 253 254 253 254 71 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 21 142 253 252
253 252 192 192 253 232 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 21 173 253 254 253 244 162 0 0 254 253 62 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 142 253 252
253 252 81 0 0 0 253 252 102 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 113 253 254 253 244 40 0 0 0 0 254 253
41 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 51 232
253 171 40 0 0 0 0 0 253 252 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 41 0 0 0 0 0 0 0 0
254 253 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 82 253 252 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 123 254 192 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 21 223 253 70 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 52 31 0 0 0 0
0 0 72 253 255 50 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 41 253 232 183 61 0 0 21 142 233 252 172 10 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 214 253 255 253
255 253 255 253 255 213 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 10 91 151 151 213 252 253 212 91 10 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0]
# Save the data files into a format compatible with CNTK text reader
def savetxt(filename, ndarray,type):
dir = os.path.dirname(filename)
if not os.path.exists(dir):
os.makedirs(dir)
if not os.path.isfile(filename):
print("Saving", filename )
with open(filename, 'w') as f:
labels = list(map(' '.join, np.eye(10, dtype=np.uint).astype(str)))
if type==1:
for row in ndarray:
row_str = row.astype(str)
label_str = labels[row[0]]
feature_str = ' '.join(row_str[1:])
f.write('|labels {} |features {}\n'.format(label_str, feature_str))
else:
for row in ndarray:
row_str = row.astype(str)
feature_str = ' '.join(row_str[1:])
f.write('|features {}\n'.format(feature_str))
else:
print("File already exists", filename)
# Save the train and test files (prefer our default path for the data)
data_dir = os.path.join("..", "Examples", "Image", "DataSets", "MNIST")
if not os.path.exists(data_dir):
data_dir = os.path.join("digitdata", "MNIST")
print ('Writing train text file...')
savetxt(os.path.join(data_dir, "Train.txt"), train,1)
print('Done')
print ('Writing test text file...')
savetxt(os.path.join(data_dir, "Test.txt"), test,0)
print('Done')
Writing train text file...
Saving digitdata/MNIST/Train.txt
Done
Writing test text file...
Saving digitdata/MNIST/Test.txt
Done
Logistic Regression
Logistic Regression(LR) is a fundamental machine learning technique that uses a linear weighted combination of features and generates probability-based predictions of different classes.
There are two basic forms of LR: Binary LR (with a single output that can predict two classes) and multiclass LR (with multiple outputs, each of which is used to predict a single class).

In Binary Logistic Regression (see top of figure above), the input features are each scaled by an associated weight and summed together. The sum is passed through a squashing (aka activation) function and generates an output in [0,1]. This output value is then compared with a threshold (such as 0.5) to produce a binary label (0 or 1), predicting 1 of 2 classes. This technique supports only classification problems with two output classes, hence the name binary LR. In the binary LR example shown above, the sigmoid function is used as the squashing function.
In Multiclass Linear Regression (see bottom of figure above), 2 or more output nodes are used, one for each output class to be predicted. Each summation node uses its own set of weights to scale the input features and sum them together. Instead of passing the summed output of the weighted input features through a sigmoid squashing function, the output is often passed through a softmax function (which in addition to squashing, like the sigmoid, the softmax normalizes each nodes’ output value using the sum of all unnormalized nodes). (Details in the context of MNIST image to follow)
We will use multiclass LR for classifying the MNIST digits (0-9) using 10 output nodes (1 for each of our output classes). In our approach, we will move the softmax function out of the model and into our Loss function used in training
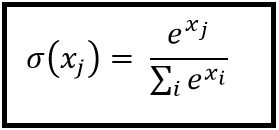
C.__version__
'2.0'
# Select the right target device when this notebook is being tested:
if 'TEST_DEVICE' in os.environ:
if os.environ['TEST_DEVICE'] == 'cpu':
C.device.try_set_default_device(C.device.cpu())
else:
C.device.try_set_default_device(C.device.gpu(0))
# Ensure we always get the same amount of randomness
np.random.seed(0)
C.cntk_py.set_fixed_random_seed(1)
C.cntk_py.force_deterministic_algorithms()
# Define the data dimensions
input_dim = 784
num_output_classes = 10
Earlier,the data was downloaded and written to 2 CTF (CNTK Text Format) files, 1 for training, and 1 for testing. Each line of these text files takes the form(for test set labels doesn’t exist):
|labels 0 0 0 1 0 0 0 0 0 0 |features 0 0 0 0 ...
(784 integers each representing a pixel)
We are going to use the image pixels corresponding the integer stream named “features”. We define a create_reader function to read the training and test data using the CTF deserializer
# Read a CTF formatted text (as mentioned above) using the CTF deserializer from a file
def create_reader(path, is_training, input_dim, num_label_classes,base):
if base==1:
labelStream = C.io.StreamDef(field='labels', shape=num_label_classes, is_sparse=False)
featureStream = C.io.StreamDef(field='features', shape=input_dim, is_sparse=False)
deserailizer = C.io.CTFDeserializer(path, C.io.StreamDefs(labels = labelStream, features = featureStream))
else:
featureStream = C.io.StreamDef(field='features', shape=input_dim, is_sparse=False)
deserailizer = C.io.CTFDeserializer(path, C.io.StreamDefs(features = featureStream))
return C.io.MinibatchSource(deserailizer,
randomize = is_training, max_sweeps = C.io.INFINITELY_REPEAT if is_training else 1)
# Ensure the training and test data is generated and available for this lab.
# We search in two locations in the toolkit for the cached MNIST data set.
data_found = False
for data_dir in [os.path.join("..", "Examples", "Image", "DataSets", "MNIST"),
os.path.join("digitdata", "MNIST")]:
train_file = os.path.join(data_dir, "Train.txt")
test_file = os.path.join(data_dir, "Test.txt")
if os.path.isfile(train_file) and os.path.isfile(test_file):
data_found = True
break
if not data_found:
raise ValueError("Please generate the data by completing Lab1_MNIST_DataLoader")
print("Data directory is {0}".format(data_dir))
Data directory is digitdata/MNIST
Model Creation
LR is a simple linear model that takes as input, a vector of numbers describing the properties of what we are classifying (also known as a feature vector, , the pixels in the input MNIST digit image) and emits the evidence . For each of the 10 digits, there is a vector of weights corresponding to the input pixels as show in the figure. These 10 weight vectors define the weight matrix with dimension of 10 x 784. Each feature in the input layer is connected with a summation node by a corresponding weight (individual weight values from the matrix). Note there are 10 such nodes, 1 corresponding to each digit to be classified. The first step is to compute the evidence for an observation.
where is the weight matrix of dimension 10 x 784 and is known as the bias vector with lenght 10, one for each digit.
The evidence is not squashed (hence no activation). Instead the output is normalized using a softmax
input = C.input_variable(input_dim)
label = C.input_variable(num_output_classes)
Logistic Regression network setup
The CNTK Layers module provides a Dense function that creates a fully connected layer which performs the above operations of weighted input summing and bias addition.
def create_model(features):
with C.layers.default_options(init = C.glorot_uniform()):
r = C.layers.Dense(num_output_classes, activation = None)(features)
return r
# Scale the input to 0-1 range by dividing each pixel by 255.
input_s = input/255
z = create_model(input_s)
Training
Below, we define the Loss function, which is used to guide weight changes during training.
We minimize the cross-entropy between the label and predicted probability by the network.
Evaluation
Below, we define the Evaluation (or metric) function that is used to report a measurement of how well our model is performing.
For this problem, we choose the classification_error() function as our metric, which returns the average error over the associated samples (treating a match as “1”, where the model’s prediction matches the “ground truth” label, and a non-match as “0”).
loss = C.cross_entropy_with_softmax(z, label)
label_error = C.classification_error(z, label)
Configure training
The trainer strives to reduce the loss function by different optimization approaches, [Stochastic Gradient Descent][] (sgd) being one of the most popular. Typically, one would start with random initialization of the model parameters. The sgd optimizer would calculate the loss or error between the predicted label against the corresponding ground-truth label and using [gradient-decent][] generate a new set model parameters in a single iteration.
The aforementioned model parameter update using a single observation at a time is attractive since it does not require the entire data set (all observation) to be loaded in memory and also requires gradient computation over fewer datapoints, thus allowing for training on large data sets. However, the updates generated using a single observation sample at a time can vary wildly between iterations. An intermediate ground is to load a small set of observations and use an average of the loss or error from that set to update the model parameters. This subset is called a minibatch.
With minibatches, we sample observations from the larger training dataset. We repeat the process of model parameters update using different combination of training samples and over a period of time minimize the loss (and the error metric). When the incremental error rates are no longer changing significantly or after a preset number of maximum minibatches to train, we claim that our model is trained.
One of the key optimization parameters is called the learning_rate.Its a scaling factor that modulates how much we change the parameters in any iteration.
# Instantiate the trainer object to drive the model training
learning_rate = 0.2
lr_schedule = C.learning_rate_schedule(learning_rate, C.UnitType.minibatch)
learner = C.sgd(z.parameters, lr_schedule)
trainer = C.Trainer(z, (loss, label_error), [learner])
# Define a utility function to compute the moving average sum.
# A more efficient implementation is possible with np.cumsum() function
def moving_average(a, w=5):
if len(a) < w:
return a[:] # Need to send a copy of the array
return [val if idx < w else sum(a[(idx-w):idx])/w for idx, val in enumerate(a)]
# Defines a utility that prints the training progress
def print_training_progress(trainer, mb, frequency, verbose=1):
training_loss = "NA"
eval_error = "NA"
if mb%frequency == 0:
training_loss = trainer.previous_minibatch_loss_average
eval_error = trainer.previous_minibatch_evaluation_average
if verbose:
print ("Minibatch: {0}, Loss: {1:.4f}, Error: {2:.2f}%".format(mb, training_loss, eval_error*100))
return mb, training_loss, eval_error
# Initialize the parameters for the trainer
minibatch_size = 64
num_samples_per_sweep = 42000
num_sweeps_to_train_with = 10
num_minibatches_to_train = (num_samples_per_sweep * num_sweeps_to_train_with) / minibatch_size
# Create the reader to training data set
reader_train = create_reader(train_file, True, input_dim, num_output_classes,1)
# Map the data streams to the input and labels.
input_map = {
label : reader_train.streams.labels,
input : reader_train.streams.features
}
# Run the trainer on and perform model training
training_progress_output_freq = 500
plotdata = {"batchsize":[], "loss":[], "error":[]}
for i in range(0, int(num_minibatches_to_train)):
# Read a mini batch from the training data file
data = reader_train.next_minibatch(minibatch_size, input_map = input_map)
trainer.train_minibatch(data)
batchsize, loss, error = print_training_progress(trainer, i, training_progress_output_freq, verbose=1)
if not (loss == "NA" or error =="NA"):
plotdata["batchsize"].append(batchsize)
plotdata["loss"].append(loss)
plotdata["error"].append(error)
Minibatch: 0, Loss: 2.4340, Error: 85.94%
Minibatch: 500, Loss: 0.2244, Error: 4.69%
Minibatch: 1000, Loss: 0.2056, Error: 6.25%
Minibatch: 1500, Loss: 0.3837, Error: 14.06%
Minibatch: 2000, Loss: 0.3418, Error: 10.94%
Minibatch: 2500, Loss: 0.2255, Error: 7.81%
Minibatch: 3000, Loss: 0.2620, Error: 7.81%
Minibatch: 3500, Loss: 0.2027, Error: 6.25%
Minibatch: 4000, Loss: 0.3416, Error: 10.94%
Minibatch: 4500, Loss: 0.2901, Error: 9.38%
Minibatch: 5000, Loss: 0.2771, Error: 7.81%
Minibatch: 5500, Loss: 0.2184, Error: 4.69%
Minibatch: 6000, Loss: 0.2237, Error: 9.38%
Minibatch: 6500, Loss: 0.4064, Error: 15.62%
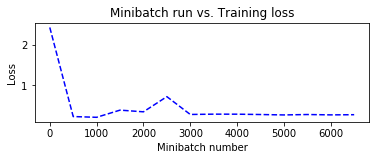
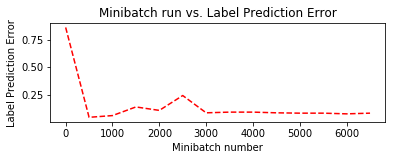
Let us plot the errors over the different training minibatches. Note that as we progress in our training, the loss decreases though we do see some intermediate bumps.
# Compute the moving average loss to smooth out the noise in SGD
plotdata["avgloss"] = moving_average(plotdata["loss"])
plotdata["avgerror"] = moving_average(plotdata["error"])
# Plot the training loss and the training error
import matplotlib.pyplot as plt
plt.figure(1)
plt.subplot(211)
plt.plot(plotdata["batchsize"], plotdata["avgloss"], 'b--')
plt.xlabel('Minibatch number')
plt.ylabel('Loss')
plt.title('Minibatch run vs. Training loss')
plt.show()
plt.subplot(212)
plt.plot(plotdata["batchsize"], plotdata["avgerror"], 'r--')
plt.xlabel('Minibatch number')
plt.ylabel('Label Prediction Error')
plt.title('Minibatch run vs. Label Prediction Error')
plt.show()
Evaluation and Submission
Now that we have trained the network, let us evaluate the trained network on the test data. This is done using trainer.test_minibatch.
# Read the testingdata
reader_test = create_reader(test_file, False, input_dim, num_output_classes,0)
test_input_map = {
input : reader_test.streams.features,
}
# Test data for trained model
test_minibatch_size = 28000
num_samples = 28000
num_minibatches_to_test = num_samples // test_minibatch_size
test_result = 0.0
for i in range(num_minibatches_to_test):
# We are loading test data in batches specified by test_minibatch_size
# Each data point in the minibatch is a MNIST digit image of 784 dimensions
# with one pixel per dimension that we will encode / decode with the
# trained model.
data = reader_test.next_minibatch(test_minibatch_size,input_map = test_input_map)
img_data = data[input].asarray()
# Average of evaluation errors of all test minibatches
print("done")
done
out = C.softmax(z)
predicted_label_prob = [out.eval(img_data[i]) for i in range(len(img_data))]
pred = [np.argmax(predicted_label_prob[i]) for i in range(len(predicted_label_prob))]
print("Predicted for 1-25:", pred[0:24])
Predicted for 1-25: [2, 0, 9, 9, 3, 7, 0, 3, 0, 3, 5, 7, 4, 0, 4, 3, 3, 5, 9, 0, 9, 1, 1, 5]
# Plot a random image
sample_number = 4
plt.imshow(img_data[sample_number].reshape(28,28), cmap="gray_r")
plt.axis('off')
img_pred = pred[sample_number]
print("Image Label: ", img_pred)
Image Label: 3
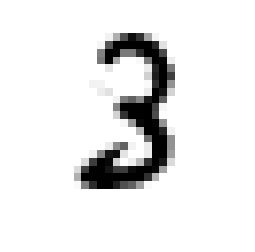
import pandas as pd
submission = pd.concat([pd.Series(range(1,28001),name = "ImageId"), pd.Series(pred,name="Label")],axis = 1)
submission.to_csv("CNTK_softmax_log.csv",index=False)
We get kaggle score of 0.91957, our logistic with softmax performs below other deeplearning submission in the leaderboard.In part 2 of the series we will use Multi layer perceptron which can learn interactions between features to create better models. Stay Tuned

Leave a Comment